Public Key vs Private Key: Understanding Cryptography in Simple Terms

How Banks Do Authentication:

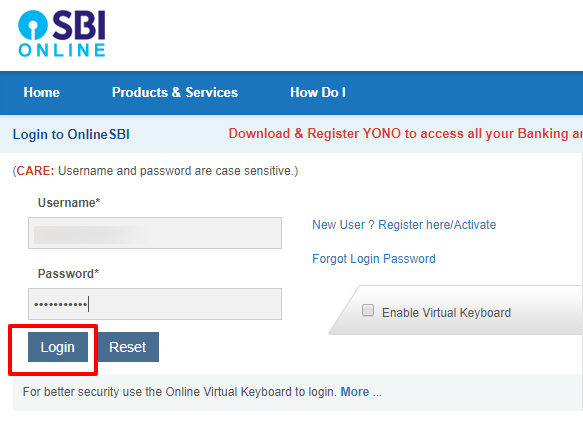
• Username and Password:

  • Traditional banks rely on a username and password for authentication.

  • These credentials allow you to:

    • View your funds.

    • Transfer funds.

    • Review your transaction history and some other features.

How Blockchains Do Authentication:

Public-Private Keypair:

Blockchain accounts are secured through a public-private keypair.

• A public-private keypair consists of two keys used in asymmetric cryptography.

Public Key:

• The public key is a string that can be shared openly with anyone.

• It acts like your "account number" on the blockchain.

• Example: Ethereum Address on Etherscan

Private Key:

• The private key is a secret string that must be kept confidential.

• It is used to sign transactions and prove ownership of the associated public key.

• Never share your private key with anyone.

---

Bits and Bytes

Why Learning this ?

• Private keys are stored in a certain format whenever you use or generate them.

• They are stored/generated in bits and bytes.

• Understanding bits and bytes, and various encoding-decoding helps when dealing with and understanding private keys.

What is a Bit?

• A bit is the smallest unit of data in a computer.

• It can have one of two values: 0 or 1.

• All programs and code you write are eventually converted to 0's and 1's.

• Analogy:

  • Think of a bit like a light switch that can either be off (0) or on (1).

• Bit Representation in JavaScript:

  •     const x = 0;
        console.log(x); // Outputs: 0
    

  • Here, x represents a single bit with a value of 0.

What is a Byte?

• A byte is a group of 8 bits.

• It’s the standard unit of data used to represent a single character in memory.

• Possible Values:

  • Since each bit can be either 0 or 1, a byte can have 2^8 (256) possible values, ranging from 0 to 255.

  • Example: The binary sequence 11001010 represents a specific value in decimal (we'll cover this in the assignment below).

• Byte Representation:

  •     const x = 202;
        console.log(x); // Outputs: 202
    

  • Here, x is a byte, representing the decimal value 202, which is equivalent to 11001010 in binary.

• Array of Bytes:

  •     const bytes = [202, 244, 1, 23];
        console.log(bytes); // Outputs: [202, 244, 1, 23]
    

  • This is an array containing multiple bytes.

Using UInt8Array in JavaScript:

• Definition:

  • UInt8Array is a typed array in JavaScript that represents an array of 8-bit unsigned integers (bytes).

• Advantages:

  • Memory Efficiency: Uses less space; each value takes only 1 byte.

  • Constraints: Ensures that values don’t exceed 255, which is the maximum value a byte can hold.

• Example:

  •     let bytes = new Uint8Array([0, 255, 127, 128]);
        console.log(bytes); // Outputs: Uint8Array(4) [ 0, 255, 127, 128 ]
    

  • This code creates a UInt8Array with four bytes, ensuring that each value stays within the valid byte range.

• Example:

  •     const binaryRepresentation = new TextEncoder().encode("h");
        console.log(binaryRepresentation); // Uint8Array(1)[104]
    

---

Why Use UInt8Array Over Native Arrays?

• Memory Efficiency:

  • Native arrays in JavaScript store numbers using 64 bits (8 bytes) per number, regardless of the actual size of the number.

  • UInt8Array stores each number using only 1 byte, which is sufficient for values between 0 and 255.

• Constraints:

  • UInt8Array enforces that each element doesn’t exceed 255, preventing potential overflow errors.

---

Encodings

• When working with computers, data is often represented in a format that is not human-readable, such as binary or bytes.

• Encoding is the process of converting this data into a more readable format.

• Some common encodings include ASCII, Hex, Base64, and Base58.

• These encodings help us represent binary data in a more understandable way.

1. ASCII (American Standard Code for Information Interchange)

• 1 character = 7 bits

• ASCII is one of the oldest encodings used to represent text in computers. Each character in ASCII corresponds to a specific number (ranging from 0 to 127), which is represented in binary.

• For example, the letter 'A' is represented by the number 65 in ASCII, which is 01000001 in binary.

ASCII table - Table of ASCII codes, characters and symbols (ascii-code.com) HTML ASCII Reference (w3schools.com)

2. Hexadecimal (Hex)

• 1 character = 4 bits

• Hexadecimal is a base-16 encoding system that uses 16 characters: 0-9 and A-F. It is commonly used in programming and digital systems to represent binary data in a more compact and readable format.

• Each hex digit represents four bits (a nibble), and two hex digits represent one byte.

💡Hex (Base16) encoder & decoder, a simple online tool 🧰 (hexator.com)

3. Base64

• 1 character = 6 bits

• Base64 is an encoding scheme that represents binary data in an ASCII string format. It uses 64 different characters (A-Z, a-z, 0-9, +, /). It is commonly used in data transfer, encoding images, and storing complex data as text.

💡Base64 Encode/DecodeBase64 Decode/Encode

4. Base58

• Base58 is similar to Base64 but uses a different set of characters to avoid visually similar characters (e.g., 0 and O, l and 1) and to make the encoded output more user-friendly.

• It is often used in Bitcoin and other cryptocurrencies for encoding addresses and other data.

---

Hashing vs Encryption

Hashing

• Hashing converts data into a fixed-size string of characters, known as a hash.

• Key points:

  • Deterministic: The same input will always produce the same hash.

  • Fixed Size: Regardless of the input size, the output hash will always be the same length.

  • One-Way Function: Hashes cannot be reversed to retrieve the original input data.

  • Collision Resistance: It is computationally difficult to find two different inputs that produce the same hash.

• Common Hashing Algorithms:

  • SHA-256: Widely used in blockchain technology, ensuring data integrity.

  • MD5: Once popular for checksums, now considered insecure due to vulnerabilities.

Encryption

• Encryption converts plaintext into ciphertext using an algorithm and a key.

• Key points:

  • Reversible: With the correct key, the ciphertext can be decrypted back to plaintext.

  • Key-Dependent: The security of encryption relies on the secrecy of the key.

Types of Encryptions:

1. Symmetric Encryption:

• Definition: The same key is used for both encryption and decryption.

• Common Algorithms:

  • AES (Advanced Encryption Standard)

  • DES (Data Encryption Standard)

💡AES Encryption and Decryption Online (devglan.com)

2. Asymmetric Encryption:

Uses a pair of keys – a public key and a private key – for encryption and decryption.

• Key Pair:

  • Public Key: Can be shared openly and is used to encrypt data.

  • Private Key: Must be kept confidential and is used to decrypt data encrypted with the corresponding public key.

• Common Algorithms:

  • RSA (Rivest–Shamir–Adleman)

  • ECC (Elliptic Curve Cryptography) - Used by ETH and BTC

  • EdDSA (Edwards-curve Digital Signature Algorithm) - Used by SOL

• Common Elliptic Curves:

  • secp256k1: Used in Bitcoin (BTC) and Ethereum (ETH).

  • ed25519: Used in Solana (SOL).

  • 

💡How Elliptic Curves Work

• Use Cases of Public-Key Cryptography:

  • SSL/TLS Certificates: Ensuring secure communication over the internet.

  • SSH Keys: For secure server access or pushing code to GitHub.

  • Blockchains and Cryptocurrencies: Ensuring secure and verifiable transactions.

A message on the blockchain is signed using private key. - A miner verifies the transaction using the signature and public key. - Public/Private Keys & Signing - Blockchain Demo: Public / Private Keys & Signing (andersbrownworth.com)

Creating a public/private keypair

Hierarchical Deterministic (HD) Wallet

HD wallets generate a tree of key pairs from a single seed, allowing users to manage multiple addresses from one root seed.

Problem:

• Traditionally, maintaining multiple wallets required storing multiple public-private key pairs.

• This is cumbersome and risky, as losing any one of these keys can result in the loss of associated funds.

Solution - BIP-32:

• Bitcoin Improvement Proposal 32 (BIP-32), introduced by Bitcoin Core developer Pieter Wuille in 2012, addresses this problem by standardizing the derivation of private and public keys from a single master seed.

• BIP-32 introduced the concept of hierarchical deterministic (HD) wallets, which use a tree-like structure to manage multiple accounts easily.

How to Create an HD Wallet

Mnemonics

• A mnemonic phrase, or seed phrase, is a human-readable sequence of words used to generate a cryptographic seed.

• BIP-39(Improvement to BIP-32) defines how mnemonic phrases are generated and converted into a seed.

Example Code to Generate a Mnemonic:

import { generateMnemonic } from 'bip39';

// Generate a 12-word mnemonic
const mnemonic = generateMnemonic();
console.log('Generated Mnemonic:', mnemonic);

Reference:

• BIP-39

• YouTube Reference

Seed Phrase

• The seed is a binary number derived from the mnemonic phrase. This seed is used to generate the master private key.

Example Code to Generate a Seed from a Mnemonic:

import { generateMnemonic, mnemonicToSeedSync } from "bip39";

const mnemonic = generateMnemonic();
console.log("Generated Mnemonic:", mnemonic);
const seed = mnemonicToSeedSync(mnemonic);

Derivation Paths

• Derivation paths specify a systematic way to derive various keys from the master seed.

• They allow users to recreate the same set of addresses and private keys from the seed across different wallets, ensuring interoperability and consistency.

• A derivation path is typically expressed in a format like m / purpose' / coin_type' / account' / change / address_index.

  • m: Refers to the master node, or the root of the HD wallet.

  • purpose: A constant that defines the purpose of the wallet (e.g., 44' for BIP44, which is a standard for HD wallets).

  • coin_type: Indicates the type of cryptocurrency (e.g., 0' for Bitcoin, 60' for Ethereum, 501' for solana).

  • account: Specifies the account number (e.g., 0' for the first account).

  • change: This is either 0 or 1, where 0 typically represents external addresses (receiving addresses), and 1 represents internal addresses (change addresses).

  • address_index: A sequential index to generate multiple addresses under the same account and change path.

Example Code for Deriving Paths and Generating Keys:

import nacl from "tweetnacl";
import { generateMnemonic, mnemonicToSeedSync } from "bip39";
import { derivePath } from "ed25519-hd-key";
import { Keypair } from "@solana/web3.js";

const mnemonic = generateMnemonic();
const seed = mnemonicToSeedSync(mnemonic);
for (let i = 0; i < 4; i++) {
  const path = `m/44'/501'/${i}'/0'`; // Derivation path for Solana
  const derivedSeed = derivePath(path, seed.toString("hex")).key;
  const secret = nacl.sign.keyPair.fromSeed(derivedSeed).secretKey;
  console.log(Keypair.fromSecretKey(secret).publicKey.toBase58());
}

---

Thing to Know

It is theoretically possible to find a 12-word recovery phrase by luck or by generating random phrases, but the probability of success is so low that it is effectively impossible.

Even with the most powerful computational resources, the time required would exceed the age of the universe by an unimaginable factor.

Cryptocurrencies rely on this extremely low probability to ensure the security of wallet keys, making it virtually impossible to guess or brute-force someone's private key or recovery phrase.